The building block of quantum computers and the simplest possible quantum system are called qubits, and this is the math you need to understand how they work.

Wavefunction

The simplest quantum system is described fully by a normalized vector \(|\psi\rangle\) in \(\mathbb{C}^2\):

\begin{equation*} |\psi\rangle = \left( \begin{matrix} a \\\
b \end{matrix} \right) = a\left|0\right \rangle+ b\left|1\right \rangle \end{equation*}

\(|a|^2 + |b|^2 = 1\) is the normalization condition, and \(\{|0\rangle, |1\rangle \}\) are basis vectors.

This vector is called a wavefunction and it represents the state of the quantum system. Now, in order to manipulate a qubit, you need to be able to change the state of the quantum system. In order to do that, you need to know which transformations are allowed. Given the normalization condition, we are constrained to unitary transformations, which are the elements of the \(\text{SU}(2)\) group. From group theory, these are generated by the elements of the algebra \(\mathfrak{su}(2)\). In this context, they are called the Pauli matrices, and they are:

\begin{equation*} \sigma_x= \left( \begin{matrix} 0 & 1 \\\
1 & 0 \end{matrix} \right) \end{equation*}

\begin{equation*} \sigma_y= \left( \begin{matrix} 0 & -i \\\
i & 0 \end{matrix} \right) \end{equation*}

\begin{equation*} \sigma_z= \left( \begin{matrix} 1 & 0 \\\
0 & -1 \end{matrix} \right) \end{equation*}

\begin{equation*} \sigma_0 = \left( \begin{matrix} 1 & 0 \\\
0 & 1 \end{matrix} \right) \end{equation*}

Now, instead of representing the system in terms of a wavefunction with complex numbers \(a\) and \(b\), it is oftentimes better to represent the system in terms of the Pauli matrices.

If we define a new vector:

\begin{equation*} \vec{\sigma} = \sigma_x\hat{x} + \sigma_y\hat{y} + \sigma_z\hat{z} \end{equation*}

in which \(\hat{x}\), \(\hat{y}\), and \(\hat{z}\) are the unit vectors of \(\mathbb{R}^3\), then we can define the Bloch vector:

\begin{equation*} \vec{n} = \left\langle \vec{\sigma} \right\rangle = \left\langle \sigma_x \right\rangle \hat{x} + \left\langle \sigma_y \right\rangle \hat{y}+ \left\langle \sigma_z \right\rangle \hat{z} \end{equation*}

where the angle brackets denote matrix multiplication with the wavefunction, for example:

\begin{equation*} \langle \sigma_x \rangle = \langle \psi | \sigma_x | \psi \rangle = \left(\begin{matrix}a^* & b^*\end{matrix}\right) \left(\begin{matrix} 0 & 1\\\
1 & 0 \end{matrix}\right) \left(\begin{matrix} a \\\
b \end{matrix}\right) = ab^* + ba^* \end{equation*}

and \(a^*, b^*\) denotes complex conjugation.¹ This allows us to visualize the quantum system as a vector on a sphere. For example, the state \(|\psi\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\) has \(\vec{n} = \hat{x}\).

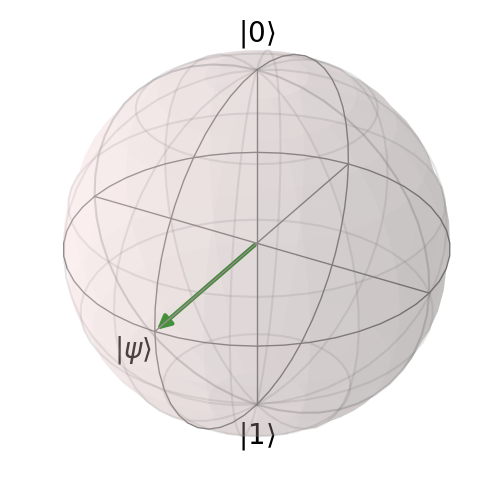
Changing the quantum state

The most general evolution of the wavefunction in time is described by multiplying the state with a unitary matrix \(U(t)\):

\begin{align*} |\psi(t)\rangle &= U(t)|\psi\rangle\\\
U(t) &= e^{-iHt} \end{align*}

where \(H\) is called the Hamiltonian. Being that the evolution is constrained to unitary transformations, we can parameterize the general transformation for a two-level system in terms of a real vector \(\vec{r}\), and the Pauli matrices:

\begin{equation*} \vec{r} = r\cos\phi\sin\theta\hat{x} + r\sin\phi\sin\theta\hat{y} + r\cos\theta\hat{z} \end{equation*}

So that the general Hamiltonian is:

\begin{equation*} H = \sigma_0r_0+ \vec{\sigma}\cdot\vec{r} \end{equation*}

\begin{equation*} H = \left( \begin{matrix} r_0 + r\cos\theta & re^{-i\phi}\sin\theta \\\
re^{i\phi}\sin\theta & r_0 - r\cos\theta \end{matrix} \right) \end{equation*}

The eigenvalues and eigenvectors of this Hamiltonian are given by:

Eigenvalues

\begin{equation*} \lambda_{1,2} = r_0 \pm r \end{equation*}

Eigenvectors

\begin{equation*} |\lambda_1\rangle = \left(\begin{matrix} \cos\frac{\theta}{2}\\\
e^{i\phi}\sin\frac{\theta}{2} \end{matrix}\right) = \cos\frac{\theta}{2}\left|0\right \rangle+ e^{i\phi}\sin\frac{\theta}{2}\left|1\right \rangle \end{equation*}

\begin{equation*} |\lambda_2\rangle = \left(\begin{matrix} e^{i\phi}\sin\frac{\theta}{2}\\\
-\cos\frac{\theta}{2} \end{matrix}\right) = e^{i\phi}\sin\frac{\theta}{2}\left|0\right \rangle-\cos\frac{\theta}{2}\left|1\right \rangle \end{equation*}

From the eigenvalues and eigenvectors, we can compute the evolution of any qubit under a general unitary transformation.

For demonstration, if we start with the initial state:

\begin{equation*} |\psi(0)\rangle = \cos\frac{\theta_0}{2}\left|0\right \rangle+ e^{i\phi_0}\sin\frac{\theta_0}{2}\left|1\right \rangle \end{equation*}

The transformed state at time \(t\) will be:

\begin{equation*} |\psi(t)\rangle = a(t)\left|0\right \rangle+ b(t)\left|1\right \rangle \end{equation*}

\begin{equation*} a(t)= i\sin(rt)\sin(\theta)\sin\frac{\theta_0}{2}e^{i(\phi_0 - \phi)} + \left[\cos(rt) - i\sin(rt)\cos(\theta)\right]\cos\frac{\theta_0}{2} \end{equation*}

\begin{equation*} b(t)= e^{i\phi_0}\left[i\sin(rt)\sin(\theta)\cos\frac{\theta_0}{2}e^{-i(\phi_0 - \phi)} + \left[\cos(rt) + i\sin(rt)\cos\theta\right]\sin\frac{\theta_0}{2}\right] \end{equation*}

And with that, we’re done! We successfully covered all possible unitary transformations of the simplest quantum system, the qubit. This is the math that underlies most quantum computers, since all real quantum computers are based on qubits.

However, since most quantum computers are imperfect, there are a number of ways that the qubits can degrade. The theory of how qubits degrade is straightforward, and I will take that up in the next post.